Computing Pi in Only One Line

I’ve always been amazed by how precisely computers can approximate Pi: the famous irrational constant 3.141592… plus infinitely more digits. Today, over 50 trillion digits have been found.

Though the value of Pi is essential to nature, Pi does not come naturally to computers. A number of algorithms are commonly used to approximate Pi, including the Gauss-Legendre, Borwein’s, and Salamin-Brent algorithms. These methods are extraordinarily efficient, but somewhat complex.

A More Straightforward Approach

There is one method — one that I discovered on my own in high school — that isn’t as fast, but is most elegant in its simple mathematic groundwork.

In calculus class, you probably studied the Taylor Series: an infinitely long summation that can model any function by matching all derivatives up to the nth degree. Our goal is to find the right Taylor Series such that the infinite summation converges to Pi itself.

Let’s start with a basic trig expression involving Pi.

$1 = tan(\frac{\pi}{4})$

Rearranging this equation allows us to solve directly for Pi.

$\pi = 4 * \arctan(1)$

Though I won’t walk through the formal derivation, the Taylor Series for 4 * arctan(1) is

$4(1 - \frac{1}{3} + \frac{1}{5} - \frac{1}{7} + ... + \frac{(-1)^n}{2n+1})$

which can be written in summation notation as

$4\sum_{n=0}^\infty \frac{(-1)^n}{2n+1}$

As you can see, this definition of Pi finds its beauty in its simplicity.

Translating to Code

The formal summation we found falls hand-in-hand with modern programming methods, as the sigma is really a for-loop in disguise.

Amazingly, the summation itself only requires 1 line of code! Using list comprehension in Python, new terms of the series generated and then accumated.

pi = 4 * sum([((-1) ** i) / (2 * i + 1) for i in range(100000)])

Though the above program is functional, the exponentiation runtime grows proportionally with i. An easy fix is using modulus to determine the next term’s sign.

pi = 4 * sum([(1 - (i % 2) * 2) / (2 * i + 1) for i in range(100000)])

Convergence and Algorithm Efficiency

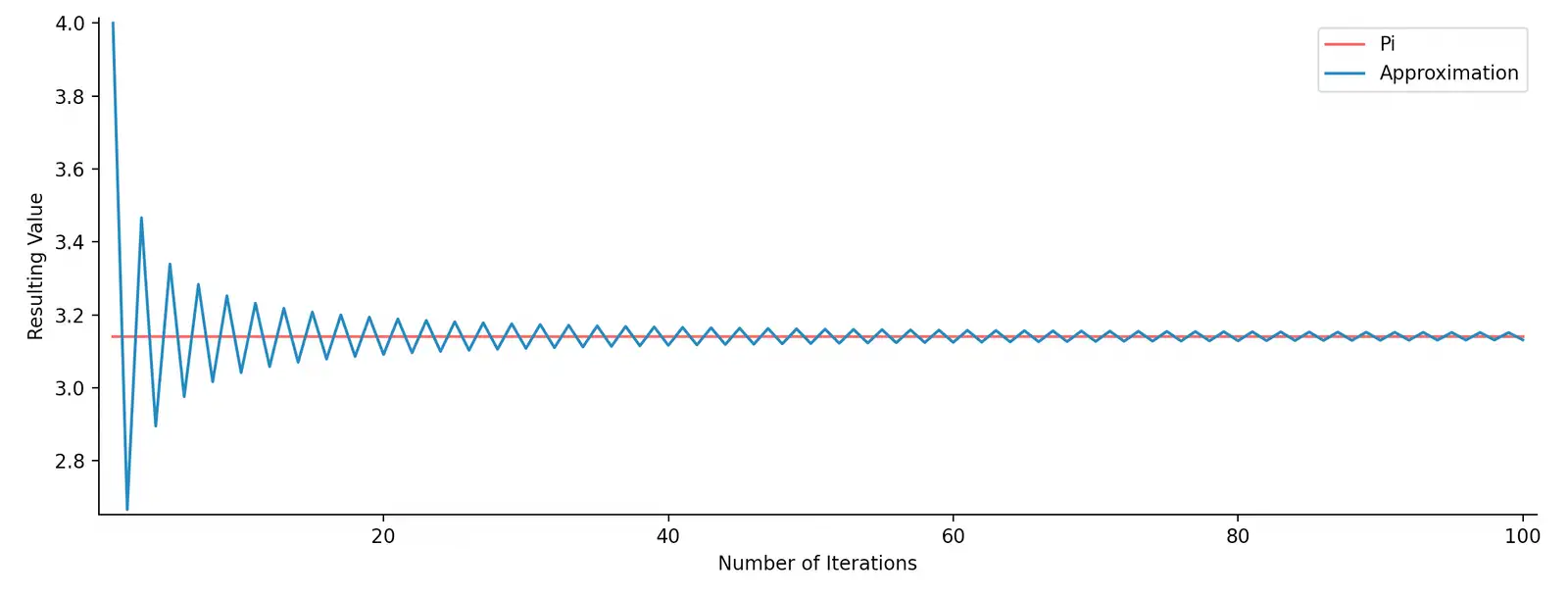
The approximation converges to Pi with increasing iterations, as visualized in this graph. Also, due to the alternating signs between terms, the approximation constantly jumps across Pi’s exact value, with each error bound being less than the previous.

Equally interesting is how the approximation’s accuracy increases with the number of iterations.

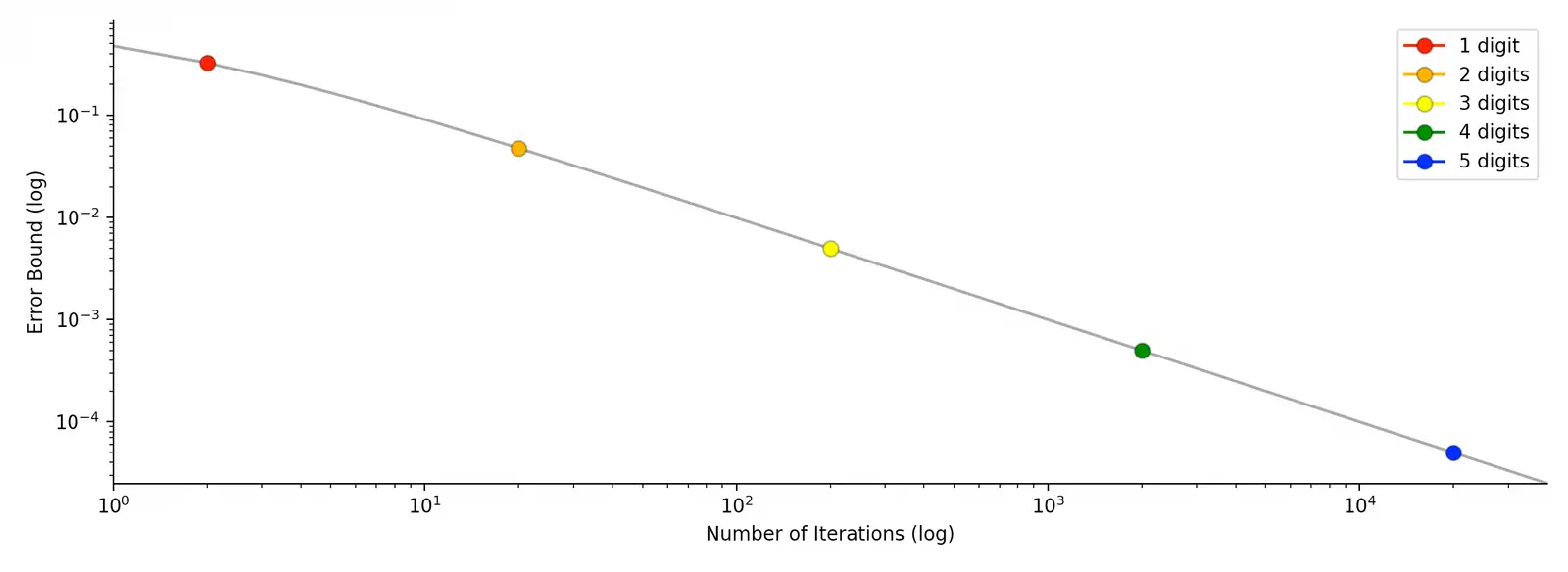
When analyzing how many iterations are required various digit of precision, I accidentally discovered that every new digit of precision occurs after the summation of 2 times a power of 10 terms (amazing coincidence, right?)!

The first digit, 3, is finalized after 2 = 2 * 10⁰ iterations, since the approximation of 2.67 is within 0.5 of Pi’s exact value. The second digit, 1, is set in stone after 20 = 2 * 10¹ iterations because 3.0916 is within 0.05 of Pi’s exact value. Following this trend, the 4 occurs after the summation of 200 terms, then the 1 after 2000 terms, then the 5 after 20,000 terms, and so on.

As exemplified by this trend, the number of operations needed to generate digits of pi grows exponentially with every digit; each digit requires 10 times more computation than the previous.

Increasing Precision

Most programming languages offer a 32-bit and 64-bit (Double) floating-point type, allowing for 7 and 16 digits of precision respectively. In other words, 3.141592653589793 is the probably the best approximation you can make out-of-the-box.

The C languages offer a Quadruple-precision floating-point type, int128, boasting up to 36 digits of precision. To compute an approximation with arbitrary (dynamic) precision, look into Java’s BigDecimal class.

Keep in mind that though languages like C and Java execute much faster than interpreted languages like Python, using larger floating-point primitives or dynamic data structures can slow down execution drastically.

Conclusion

If you want to earn the new world record for discovering the most digits of Pi, this method is not for you.

However, the algorithm outlined here is unique in its pure simplicity and mathematical elegance. Computer science is nothing but math with a keyboard, allowing us to further understand the natural world with our man-made machines.