New Year's Math Magic: Inscribing Circles Inside the Standard Parabola

Blake Sanie | Jan 1, 2022

Motivation

On New Year’s Eve, I came across a puzzling twitter post:

Traditionally, my last puzzle of the year. 🥂 🧩 ♥️{" "} #mathiratti {" "} pic.twitter.com/SVXpreN7IV
— Diego Rattaggi 🇨🇭 (@diegorattaggi) December 31, 2021

I thought, surely, the answer must be a nasty decimal - I was far from wrong, and my curiosity led me down a road to a mind-blowing realization.

Pen Meets Paper

With a bit of calculus, the answer was in close reach. To my delight, my work came out to a clean 2022. Ah, yes - only now had I realized I stumbled upon a New Years Eve joke! Still, my curiosity persisted - is this merely a coincidence, or a generalizable rule?

A Beautify Discovery

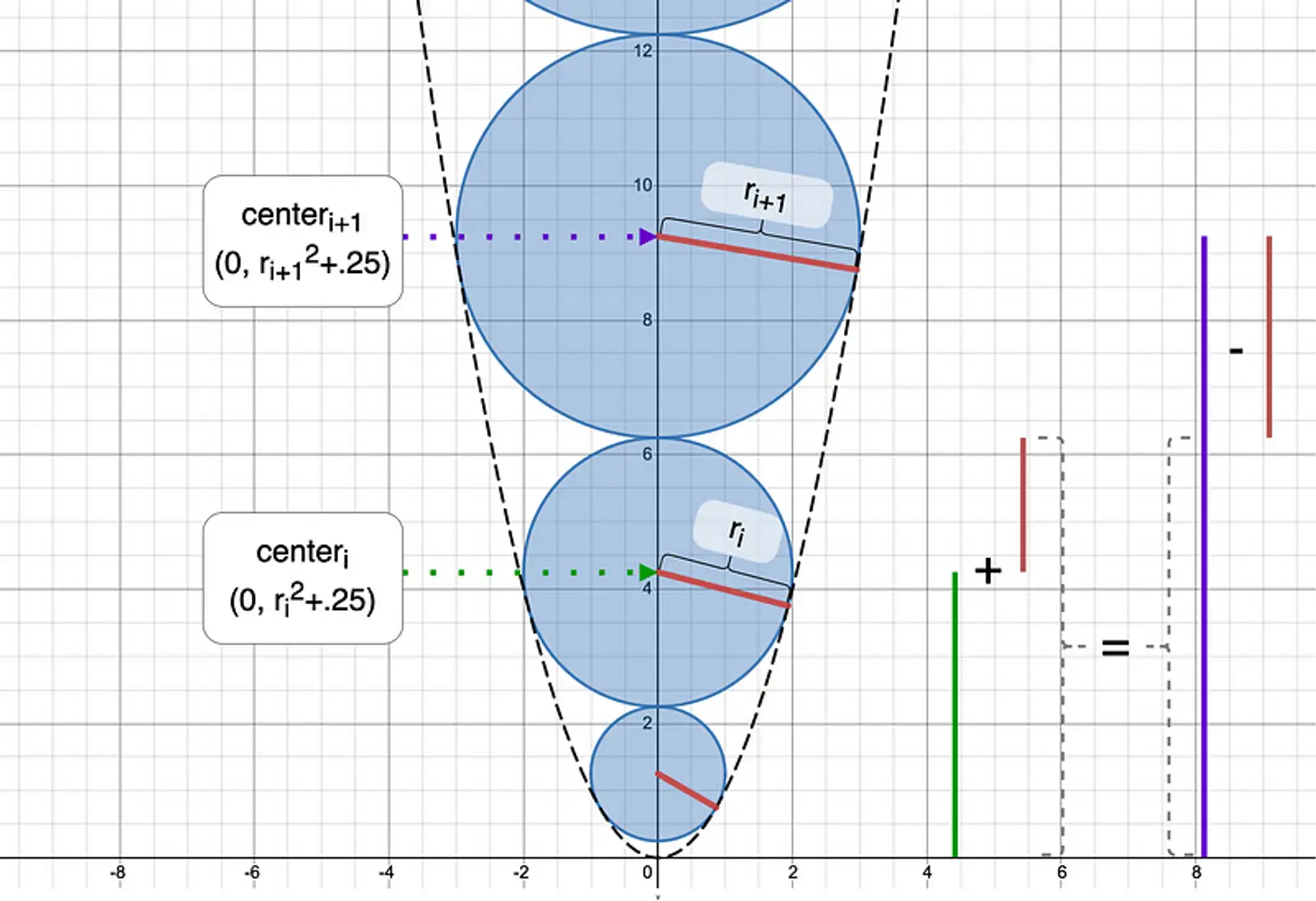
I hypothesized that for all $r>0$ , if a circle with radius $r$ is inscribed in the standard parabola, then the subsequent inscribed circle must have radius $r+1$ .

More formally, I want to determine if:

center $_i + r_i =$ center $_{i + 1} - r_{i + 1}$

for all $i>0$ , not restricted to whole numbers.

Illustration of hypothesis

The Radius Segment

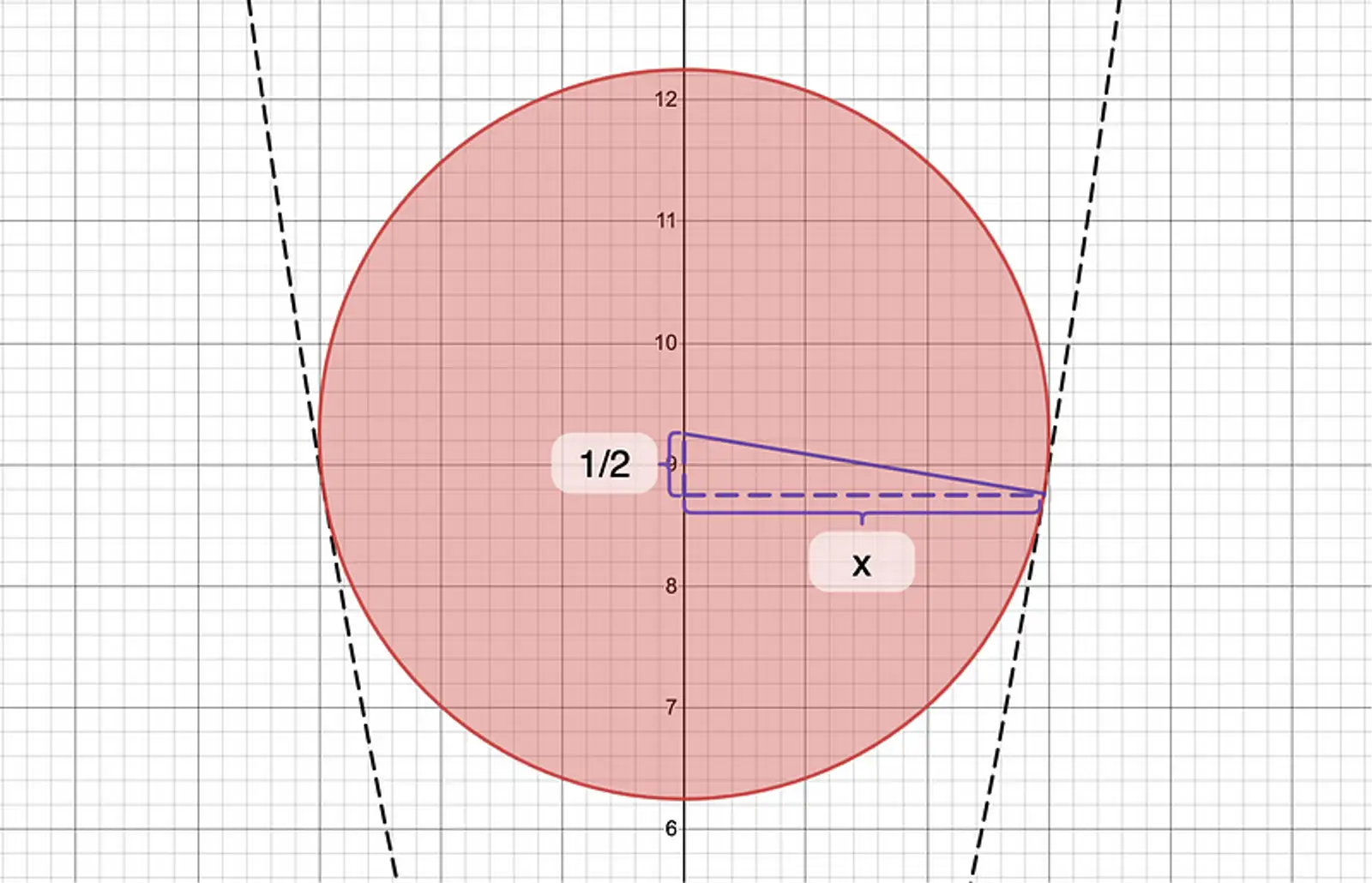
First, we must model the radius of each circle as the segment connecting (for simplicity) the $+x$ half of the standard parabola to the $y$ -axis that is simultaneously normal to such parabola.

Given this interpretation, we can find the slope of the radius by finding the negative reciprocal of the parabola’s slope.

$f(x)=x^2$ $f\prime (x)=2x$ $\downarrow$

slope of radius $=\frac{-1}{f\prime (x)}=\frac{-1}{2x}$

With this slope, we can express the radius as the sum of horizontal and vertical components. The horizontal component is, well, the definition of $x$ . The vertical component, fascinatingly, is always $1/2$ , since moving backwards $x$ units along the $x$ -axis yields a $y$ -change of $(\frac{-1}{2x}) * -x = -\frac{1}{2}$ .

Component breakdown of radius

Hence, the length of the radius is the magnitude of the resulting hypotenuse. We can calculate the $y$ -value of the center accordingly.

$r_i=\sqrt{x_i^2+\frac{1}{2}^2}$

$\downarrow$

$x_i = \sqrt{r_i^2-\frac{1}{4}}$

center $_i=f(x_i)+\frac{1} {2}=r_i^2+\frac{1} {4}$

Proof by Induction

Base Case

Fundamentally, there exists a circle of radius of radius $r > 0$ , and its center can be found by $r^2 + \frac{1} {4}$ . The circle with $r = 0$ is excluded from the domain since it constructs a point. By the way, notice anything special about the constant $\frac{1} {4}$ ? It’s the focus of the standard parabola!

Inductive Step

Having supported the base case, if we prove that our hypothesis holds true when transitioning from $i$ to $i + 1$ , then our hypothesis must hold true for all $i > 0$ .

Let’s begin by stating our hypothesis, and manipulating the relationship until a conclusion is reached.

center $_i + r_i =$ center $_{i + 1} - r_{i + 1}$

$r_i^2+\frac{1}{4}+r_i=r_{i+1}^2+\frac{1}{4}-r_{i+1}$

$r_{i+1}^2-r_{i+1}-(r_i^2+r_i)=0$

Now factor using the Quadratic Formula, where

$a=1$ $b=-1$ $c=r_i^2+r_i$

$r_{i+1}=\frac{-b \pm \sqrt{b^2-4ac}}{2a}$

$=\frac{1\pm\sqrt{1-4(r_i^2+r_i)}}{2}$

$=\frac{1\pm(2r_i+1)}{2}$

$=\cancel{r_i}, r_i+1$

$\therefore r_{i+1} = r_i+1$

In conclusion, we accept the hypotheses - the radius of every circle inscribed in the standard parabola is one greater than that of the circle underneath.

😂 Ah, and that’s why the tweet was made “traditionally”.

What about non-standard Parabolas?

So far, we have seen that inscribing circles by the horizontal bounds of the standard parabola and circle beneath is possible for incrementing radii, starting at any non-zero radius.

Keep imagining the standard parabola with its inscribed circles. When the function becomes $f(x) = ax^2$ , where $a = 1$ does not hold, a vertical (and in a way, horizontal) stretch transformation is applied. Hence, this same transformation will be applied to the inscribed circles, yielding ellipses - the unique property of inscribed circles with incrementing radii does not hold here.

Visualization

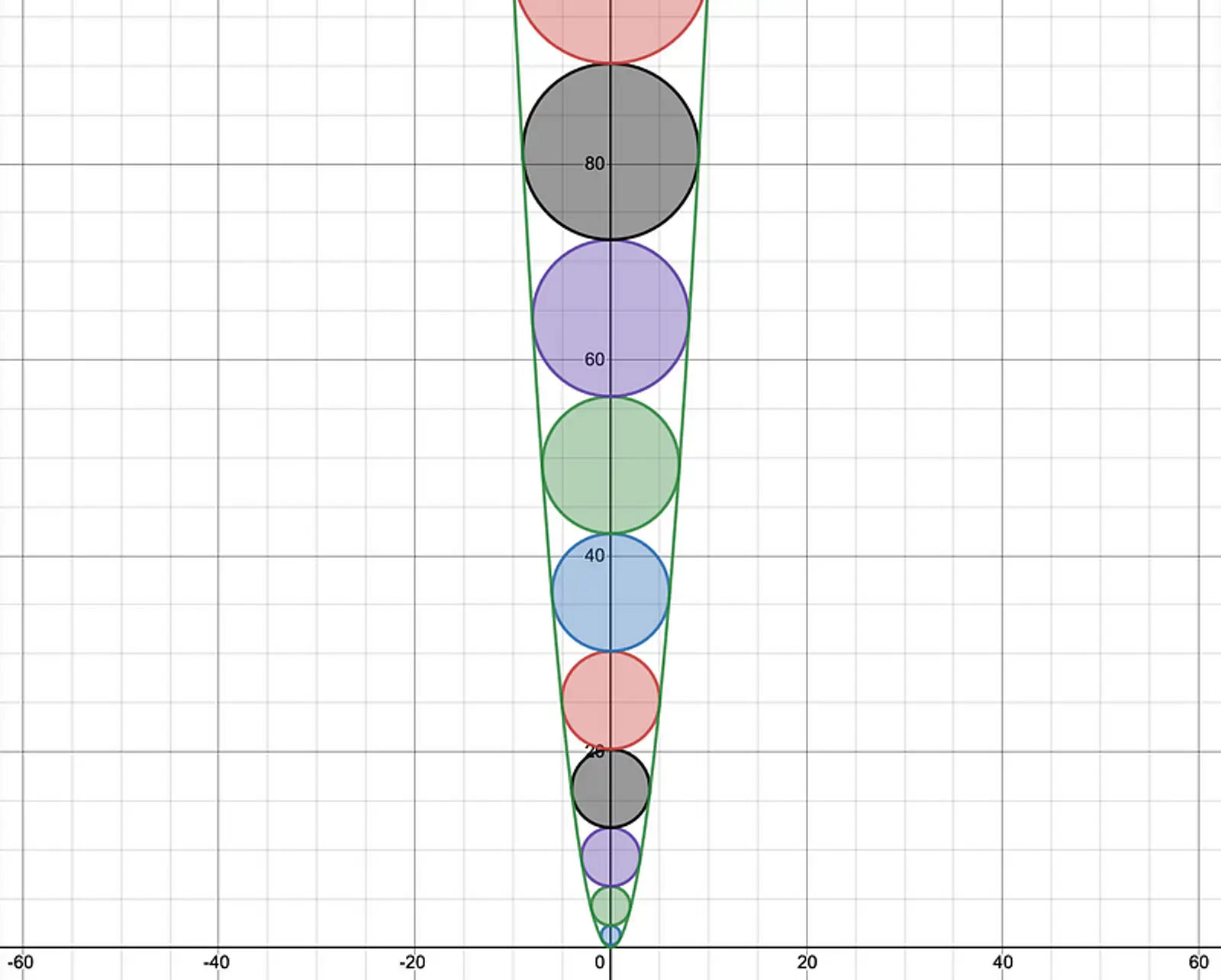
To verify my work so far, I wrote a one-line python program to generate the equations for first 20 inscribed circles of whole-number radii.

[print(f'x^2 +(y - {r}^2 - 1/4)^2 <= {r}^2') for r in range(1, 101)]

Yielding the output:

x^2 +(y - 1^2 - 1/4)^2 <= 1^2
x^2 +(y - 2^2 - 1/4)^2 <= 2^2
x^2 +(y - 3^2 - 1/4)^2 <= 3^2
...
x^2 +(y - 99^2 - 1/4)^2 <= 99^2
x^2 +(y - 100^2 - 1/4)^2 <= 100^2

Pasting into Desmos renders the beautiful phenomenon I stumbled upon to start 2022.

Final visualization of inscribed circles in standard parabola

Thanks for reading!